Java: Red-Black Tree

Порівняння TreeMap, HashMap та LinkedHashMap

Найчастіше використовують HashMap як втілення інтерфейсу Map внаслідок простоти використання і швидкого доступу до даних. Але інколи необхідно зберігати дані у структурованому вигляді для ефективної навігації. У такому випадку використовують TreeMap, що втілює інтерфейс NavigableMap, успадкований від SortedMap, а той, у свою чергу, від інтерфейсу Map — див. схему нижче, на якій чорними лініями вказано наслідування, а червоними — втілення.

інтерфейс Map ┌───┘ │ └───┐ інтерфейс │ клас SortedMap │ Hashtable │ клас │ HashMap інтерфейс │ NavigableMap │ │ клас │ LinkedHashMap клас TreeMap

Втілюючи інтерфейси NavigableMap і SortedMap, TreeMap отримує додатковий функціонал, якого немає в HashMap. Але платою за це продуктивність. Час доступу до елементів TreeMap найтриваліший. Якщо не потрібно зберігати дані в упорядкованому вигляді, краще використати HashMap або LinkedHashMap.

Клас LinkedHashMap дозволяє зберігати дані у порядку додавання. Спільні й відмінні риси цих трьох класів подано такою таблицею.

	HashMap	LinkedHashMap	TreeMap
Порядок зберігання даних.	Випадковий	У порядку додавання	У порядку зростання
Час доступу до елемента	O(1)	O(1)	O(log(n))
Імплементовані інтерфейси	Map	Map	NavigableMap, SortedMap, Map
Основа втілення (структури даних)	Відра (buckets)	Відра (buckets)	Червоно-чорне дерево (Red-Black Tree)
Використання ключа null	Можна	Можна	Лише при використанні порівнювача, що дозволяє null
Потоко- безпечність	Ні	Ні	Ні

У цій таблиці використано такі поняття.

Відра (англійською buckets) — групи, на які поділяють елементи структури даних і які потім упорядковують окремо.
Червоно-чорне дерево (англійською red-black tree) — двійкове (бінарне) дерево пошуку, кожний вузол (вершина) якого має додаткове поле, що містить колір — червоний або чорний — і що має такі властивості:
Кожний вузол є або червоним, або чорним.
Кореневий вузол є чорним (не всі автори вважають це обов'язковим).
Усі листкові вузли чорні.
Якщо вузол червоний, обидві його дочірні частини чорні.
Довільний шлях від кореневого вузла до листового вузла має однакову кількість чорних вузлів.
Щодо терміну двійкове дерево пошуку нагадаємо таке.

Двійкове дерево — структура даних у вигляді дерева орієнтованого графа, в якому з кожної вершини (вузла) виходить не більше двох дуг (орієнтованих ребер).

Зазвичай такі графи подають рисунком, на якому корінь — вершину, яка не є кінцем жодної дуги — зображують вгорі, а вектори, що відображають дуги, спрямовано вниз-ліворуч або вниз-праворуч. Вершини, у які спрямовані ці дуги, називають відповідно лівим і правим нащадками вершини, з якої виходять ці дуги, а двійкові дерева, що є частинами початкового двійкового дерева з коренями у цих нащадках — лівим і правим піддеревами.
Двійкове дерево пошуку (англіською binary search tree, BST) — двійкове дерево, у якому:
для кожного вузла (вершини) визначено ключ — деяку величину;
на множині значень ключів визначено операцію порівняння "менше";
справджуються такі висловлювання — властивості дерева пошуку:
для довільного вузла X:
у всіх вузлів лівого піддерева значення ключів менші, ніж значення ключа даних X;
у всіх вузлів правого піддерева значення ключів не менші, ніж значення ключа даних X;
усі піддерева — ліві та праві — є двійковими деревами пошуку.

На малюнку нижче подано зображення двійкового дерева пошуку, запозичене зі сторінки https://en.wikipedia.org/wiki/Binary_search_tree.

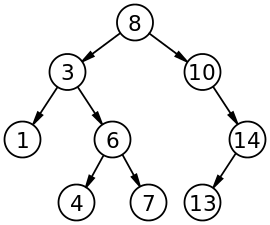
Зазвичай вузол двійкового дерева подають записом з такими полями:
- дані, прив'язані до вузла;
- посилання на лівого нащадка;
- посилання на правого нащадка;
- посилання на батьківський вузол.
У подальшому описі червоно-чорного дерева використано матеріали сторінки https://algorithmtutor.com/Data-Structures/Tree/Red-Black-Trees/.

При використанні такого дерева для зберігання пар ключ/значення:
- в усіх вузлах, крім листкових, розташовують пари;
- у чорних листкових вузлах розташовують NULL (NIL).
На малюнку нижче подано зображення червоно-чорного дерева, використаного для упорядкування пар з ключами 1, 6, 8, 11, 13, 15, 17, 22, 25, 27 і запозиченого зі сторінки https://en.wikipedia.org/wiki/Red%E2%80%93black_tree.

Чорна висона вузла — кількість чорних вузлів на шдяху від даного вузла (не рахуючи його) до вузла, обидва нащадки якого NULL (рахуючи цей вузол).

Чорна висона червоно-чорного дерева — чорна висота його кореня.

Висота червоно-чорного дерева має порядок O(log n), де n — кількість вершин. Доведемо це.
- Розглянемо випадок, коли усі вузли дерева чорні. Позначимо чорну довжину дерева через k. Маємо:
  n = 2^k – 1 ⇔ k = log₂(n + 1) = O(log n).
- Додавання червоного вузла у дерево збільшує його висоту. Отже, червоно-чорне дерево чорної висоти k має щонайменше 2^k – 1 вузлів. Червоно-чорне дерево має максимальну висоту, коли колір вузла на його найдовшому шляху змінюється при переході до наступного вузла. У цьому випадку чорна висота дерева дорівнює h/2, де h — фактична висота дерева — кількість усіх вершин, незалежно віл їхнього кольору, на шляху від кореня до вузла, обидва нащадки якого NULL. Маємо:
  n ≥ 2^h/2 − 1 ⇔ 2log₂(n + 1) ≥ h.
Серед операцій: пошук, попередник, наступник, вставлення, видалення — дві останні можуть порушити перелічені вище 5 властивостей. У цьому випадку потрібно перебудувати дерево одним з 3 способів, які мають такі назви:
- поворот ліворуч (у вузлі x); x y / \ / \ a y → x c / \ / \ b c a b
- поворот праворуч (у вузлі x); y x / \ / \ x c → a y / \ / \ a b b c
- перефарбування — зміна коліру вузла: якщо він червоний, він стає чорним і навпаки.
Операція вставлення. Щоб вставити вузол K в червоно-чорне дерево T, потрібно зробити таке.
1. Вставити К, використавши звичайне вставлення у бінарне дерево пошуку.
2. Зафарбувати К червоним кольором.
3. У разі порушення властивостей червоно-чорного дерева, виправити це, використавши перелічені три способи.
Розглянемо всі випадки вставлення, щоб пересвідчитися у можливості виправлення графу для задоволення усіх 5 властивостей червоно-чорного дерева. Використаємо такі позначення для вузлів безпосередньо після вставлення і перед виправленням:
P — батьківський вузол;
U — вузол дядька;
G — вузол дідуся.
У поданих нижче схемах (у тому числі і для операції вставлення) не відображено продовження вниз і вгору, вузол U може бути праворуч від вузла P.
1. Т — порожнє. Зробити K коренем дерева і зафарбувати його в чорний колір.
2. P — чорний. Не порушено жодну з властивостей, тому нічого додатково робити не потрібно.
3. P та U — червоні. Порушено властивість 4: P і K обидва червоні. Тоді вузол дідуся G має бути чорним, бо дерево перед вставленням має бути червоно-чорним деревом. У цьому випадку потрібно змінити кольори вузлів P, U і G: P та U стануть чорними, G стане червоним.
  G G / \ / \ U P → U P \ \ K K
  Якщо G є коренем T, не потрібно змінювати колір G, бо це порушить властивість 2.
4. P — червоний, U — чорний (у тому числі NULL), P — праворуч від G, K — праворуч від P. У цьому випадку потрібно спочатку виконати обертання ліворуч в точці G, що зробить G братом K. Далі — змінити колір G на червоний, а колір P — на чорний.
  G P P / \ / \ / \ U P → G K → G K \ / / K U U
5. P — червоний, U — чорний (у тому числі NULL), P — праворуч від G, K — ліворуч від P. У цьому випадку потрібно спочатку виконати поворот праворуч у точці P.
  G G / \ / \ / \ → / \ U P U K / \ K P
  А далі діяти так, як у попередньому випадку, із заміною K на P і навпаки.
6. P — червоний, U — чорний (у тому числі NULL), P — ліворуч від G, K — ліворуч від P. Цей випадок симетричний випадку 4, тому достатньо викоконати відповідно симетричні дії.
7. P — червоний, U — чорний (у тому числі NULL), P — ліворуч від G, K — праворуч від P. Цей випадок симетричний випадку 5, тому достатньо викоконати відповідно симетричні дії.
Операція видалення. При видаленні вузла з двома нелистовими нащадками у звичайному двійковому дереві пошуку шукають або найбільший елемент у його лівому піддереві, або найменший елемент у його правому піддереві і переміщують значення знайденого вузла у вузол, що планували видаляюти спочатку. Копіювання значення з одного вузла в інший не порушує властивостей червоно-чорного дерева, бо структуру дерева та кольори вузлів не змінено. Потім видаляють вузол, з якого копіювали значення. Цей вузол не може мати два дочірніх нелистових вузла, бо інакше він не буде найбільшим/найменшим елементом серед тих, які не перевищують / не менші від того, який видаляють. Отже, випадок видалення вузла, що має два нелистові нащадки, зводиться до випадку видалення вузла, що має не більше одного нелистового нащадка. Надалі обмежимося розглядом лише такого випадку видалення вузла А, щоб пересвідчитися у можливості виправлення графу для задоволення усіх 5 властивостей червоно-чорного дерева.
1. A є червоним вузлом. У цьому випадку видалення A не порушує жодної властивості червоно-чорного дерева.
2. A є чорним вузлом і має червоного нащадка. У цьому випадку замінюють A його червоним нащадком і змінюють колір нащадка на чорний.
  
  Примітка. Якщо A є чорним вузлом і має чорного нащадка, просте видалення чорного вузла A порушить властивість 5. На поданих нижче схемах перетворення фіолетовим кольором позначено вузли, колір яких може бути як червоним, так і чорним. Розглянуто лише випадки 3-6, коли А є лівим нащадком. Інші 4 випадки, коли А є правим нащадком, симетричні розглянутим.
3. А є чорним вузлом, має чорного предка В й червоного брата D. У цьому випадку змінюють кольори брата і предка, а потім виконують поворот ліворуч на предку B.
  B D / \ / \ / \ → / \ A D B E / \ / \ C E A C
  Таким чином задачу видалення вузла А зведено до одного з наступних трьох випадків 4-7.
4. А є чорним вузлом і має:
  червоного предка В;
  чорного брата D, обидва нащадки якого — C i E — чорні.
  Потрібно змінити:
  - колір батька В — на чорний;
  - колір брата D — на червоний,
  щоб потім вилучити А.
  B B / \ / \ / \ → / \ A D A D / \ / \ C E C E
5. А є чорним вузлом і має:
  чорного предка В;
  чорного брата D, обидва нащадки якого — C i E — чорні.
  Якщо В є коренем дерева, достатньо змінити колір брата D на червоний, щоб потім вилучити А.
  B B / \ / \ / \ → / \ A D A D / \ / \ C E C E
  Інакше після зміни кольору D на червоний потрібно поєднати вузли А і В у так званий подвійний чорний вузол і призначити цей подвійний чорний вузол для видалення. Але перед видаленням потрібно розгрупувати цей подвійний чорний вузол і видалити лише вузол А.
6. А є чорним вузлом і має чорного брата, лівий нащадок якого червоний, а правий — чорний. Потрібно змінити кольори брата D та його лівого нащадка С, виконати поворот праворуч у вузлі С й отримати дерево, розглянуте у наступному пункті 7.
  B B / \ / \ / \ → / \ A D A C / \ \ C E D \ E
7. . А є чорним вузлом і має чорного брата D, правий нащадок якого (E) — червоний. Потрібно змінити:
  - колір Е — правого нащадка брата D — на чорний;
  - колір D — на колір В — батька А;
  - колір В — на чорний
  і виконати лівий поворот у вузлі В. Після цього можна видалити чорний вузол А, щоб забезпечити задовлення усіх властивостей червоно-чорного дерева.
  B D / \ / \ / \ → / \ A D B E / \ / \ C E A C

Проілюструємо дію пункту 5 на конкретному прикладі вилучення вершини висоти 1 з найменшою координатою з дерева, що має чорну висоту 3 і містить лише 14 чорних вершин (на схемах нижче їх позначено літерами латиниці), що не є листками.┌──────G──────┐ C M / \ / \ / \ / \ A E K O \ / \ / \ / \ B D F H L N P ↓ ┌──────G──────┐ AC M / \ / \ / \ / \ B E K O / \ / \ / \ D F H L N P ↓ ┌──────G──────┐ C M / \ / \ / \ / \ B E K O / \ / \ / \ D F H L N P