Рудик Олександр Борисович,
мобільний телефон: 099 3745641,
e-mail: rudykob@gmail.com

Навчальні модулі

1. Набуття процедурної компетентності при розв'язуванні логічних задач
2. Розвиток комбінаторного мислення
3. Відношення подільності
4. Вивчення аксіом геометрії та їхніх безпо­серед­ніх наслідків
5. Набуття процедурної компетентності в опануванні алгоритмами у процесі розв’я­зання задач на по­бу­дову
6. Ефективність розв’язання та його оформлення для показникових і логарифмічних нерівностей
7. Логічно-послідовний і сучасний виклад шкільного курсу математики
8. Початки мови розмітки тексту з математичними формулами LaTeX
9. Елементи теорії груп при поглибленому вивченні математики
10. Система комп'ютерної алгебри Reduce
11. Аналіз статистичних даних і критерії прийняття гіпотез
12. Початки теорії автономних систем

Примітка. Автор курсів готовий провести очне (-i) заняття за навчальними матеріалами модуля (-ів). Необхідною умовою є надсилання листа керівника навчального закладу на адресу директора ІПО із замовленням проведення заняття з вказаного модуля для щонайменше 16 вчителів у приміщенні замовника. Вчителі можуть бути з різних навчальних закладів або районів.

Логічно-послідовний і сучасний виклад шкільного курсу математики

Анотація
Ознайомлення з причинами необхідності переходу до сучасного й логічно-послідовного вивчення математики, обгрунтування можливості цього переходу вже зараз.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — (бажано при синхронному перегляді відеозапису виступу Олександра Рудика на тематичній дискусії «Логічно-послідовний і сучасний виклад шкільного курсу математики» від 20 березня 2018 року на курсах підвищення кваліфікації вчителів математики) ознайомитися з такими матеріалами :

  • Олександр Рудик. Загальний підхід до формування переліку компетенцій щодо опанування природничо-математичними дисциплінами // Математика у сучасній школі, 2012, № 1, с. 29–32.

  • Олександр Рудик. Першочергове завдання загальної освіти України.

  • Олександр Рудик. Заява на адресу Міністра освіти і науки щодо законопроекту «Про освіту», опублікованого сайті mon.gov.ua для обговорення, вхідний № Р–5562 від 30.10.2015.

  • Олександр Рудик. Зауваження щодо проекту концепції нової української школи.

  • Проекти навчально-тематичного плану і програми вивчення математики у 5–12 класах.

    Зміст, передмова, предметний покажчик і перелік позначень посібника «Початки алгебри, аналізу, аналітичної геометрії і теорії ймовірностей» (Тернопіль: Навчальна книга — Богдан, 2005, 416 с.).

  • Посібник «Початки алгебри, аналізу, аналітичної геометрії і теорії ймовірностей» (Тернопіль: Навчальна книга — Богдан, 2005, 416 с.).

  Весь навчальний матеріал, глосарій і додатки подано у перелічених матеріалах.

• Завдання для самостійної роботи — контроль результатів навчання — подати умову завдання:

  • для якого теоретичні основи розв'язання не виходять за межі навчальної програми 1-9 класів загальноосвітнього рівня;

  • яке перевіряє уважне ставлення до умови, у тому числі, перевірку справдження умов можливості використання готових шаблонів розв'язання задач.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Вивчення аксіом геометрії та їхніх безпо­серед­ніх наслідків

Анотація
Модуль передбачає вивчення теоретичних і практичних аспек­тів методики запровадження фундаментальних понять геометрії та вивчення їхніх властивостей на належному науковому рівні.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з такими матеріалами:

  • Стаття «Загальний підхід до формування переліку компетенцій щодо опанування природничо-математичними дисциплінами» // Математика у сучасній школі, 2012, № 1, с. 29–32 — приділити увагу компетенціям щодо опанування теорією.

  • Недоліки підручників, виявлені при рецензуванні навчально-методичного комплекту з геометрії для 7–11 класів загальноосвітніх навчальних закладів — приділити увагу порушенням щодо логіки подання навчального матеріалу і використанню неозначених або некоректно означених понять у наявних підручниках.

  • Стаття «Деякі базові поняття геометрії та аксіоми геометрії» — приділити увагу першим трьом висловлюванням, що вимагають доведення.

  Весь навчальний матеріал, глосарій і додатки подано у перелічених матеріалах.

• Завдання для самостійної роботи — контроль результатів навчання: подати приклад висловлювання щодо геометричних фігур, яке:

  • видається очевидним для пересічного учня;
  • насправді вимагає доведення, якого немає у літературі з грифом МОН;
  • відсутнє серед перелічених у статті «Деякі базові поняття геометрії та аксіоми геометрії».

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Набуття процедурної компетентності при розв'язуванні логічних задач

Анотація
Модуль передбачає ознайомлення з основними методами унаочнення умови та єдиним алгоритмом розв'язання логічних задач (пошук з поверненням).

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з такими матеріалами:

  • Стаття «Загальний підхід до формування переліку компетенцій щодо опанування природничо-математичними дисциплінами» // Математика у сучасній школі, 2012, № 1, с. 29–32 — приділити увагу компетенціям щодо мовлення, роботи з символьними записами, унаочненням.

  • Умови задач логічного характеру — ознайомитися щонайменше з одним демонст­раційним розв'язанням для кожної з таких основних ідей розв'язання: повний перебір, оптимізація перебору, прямокутні табниці, непрямокутні таблиці (система прямокутних таблиць), використання відношення подільності, використання схем розташування, графи у задачах про спортивні турніри та двома задачами на дешифрацію запису дії додавання.

  • Етапи розв'язування задач з логічним навантаженням:

    1. Усвідомлення і тлумачення окремих висловлювань умови — потрібно правильно розтлумачити поняття, деталізувати запитання, знайти у тексті задачі відомості та дані, які задані в явному чи неявному вигляді. Інколи потрібно скористатися явними або неявними домовленостями: перелік персонажів у простих реченнях умови означає, що всі вони різні, кожний персонаж має одне ім'я, один фах, одне помешкання тощо.

    2. Унаочнення і структурування даних — потрібно багатослівний словесний опис подати або таблицею (однією чи кількома), або схемою розташування, або схемою сполучення, вбо рівняннями чи нерівностями, або іншим способом. Причому спосіб унаочнення має бути зручним і для подання умови, і для процесу розв'язання. Останнє означає, що таке унаочнення має допомагати вибрати наступний крок розв'вязання.

    3. Отримати відповідь, використавши єдиний спосіб розв'язання логічних задач.

    Примітка. Розв'язання більшості задач (з наявної навчальної літератури) не вимагає перебору припущень щодо невизначених значень властивостей об'єктів (див. пункти 4, 5, 6 поданого далі алгоритму). У цьому випадку виконання алгоритму зводиться лише до виконання його перших трьох пунктів. Саме такими й будуть задачі, які буде розглянуто на уроці та задано як домашнє завдання.

  • Єдиний спосіб розв'язання логічних задач
    з початковим рівнем прийняття припущень (гіпотез) 0 має такий вигляд:

    1. Зробити всі можливі висновки з умови і вже зроблених висновків, зазначаючи, що ці висновки отримано, а відповідні частини вже використано на початковому нульовому рівні.

    2. Якщо отримано відповідь, то припинити виконання алгоритму після запису відповіді.

    3. Якщо отримано суперечність, то припинити виконання алгоритму.

    4. Збільшити рівень прийняття припущень на 1.

    5. Перебрати послідовно всі можливі припущення про невизначене значення властивості одного об'єкта з умови (ім'я, фах, вік, адреса помешкання тощо).

    6. Для прийнятого припущення зробити всі можливі висновки з умови, прийнятого припущення і вже зроблених висновків, зазначаючи, що ці висновки отримано, а відповідні умови використано на даному рівні прийняття припущень. В результаті потрапити в один з таких трьох станів:

       • отримано один з варіантів відповіді. Тоді записати цей варіант відповіді, відмінити припущення найвищого рівня і всі його наслідки, після чого прийняти наступне припущення на цьому рівні й перейти до виконання пункту 6. Якщо всі припущення на даному рівні розглянуто, то зменшити рівень прийняття припущень на 1. Якщо таким чином отримано рівень 0, то припинити перебір припущень, інакше перейти на виконання пункту 5;

       • отримано суперечність. Тоді відмінити припущення найвищого рівня і всі його наслідки, після чого прийняти наступне припущення на цьому рівні й перейти до виконання пункту 6. Якщо всі припущенння на даному рівні розглянуто, то зменшити рівень прийняття припущень на 1. Якщо таким чином отримано рівень 0, то припинити перебір припущень, інакше перейти на виконання пункту 5;

       • не отримано ні відповіді, ні суперечності. Тоді збільшити рівень прийняття припущень на 1 і перейти до виконання пункту 5.

  Відсутність жодного варіанту відповіді перед припиненням алгоритму означає: умова несумісна, тобто розв'язків немає.

  Весь навчальний матеріал, глосарій і додатки подано у перелічених матеріалах.

• Завдання для самостійної роботи — контроль результатів навчання — вказати хоча б для двох розглянутих задач, скільки є рівнів прийняття гіпотези і скільки гіпотез є на кожному рівні для наявних демонстраційних розв'язань при аналізі істина / хибність кожної гіпотези незалежно одна від одної. Подані відповіді для задач мають відрізнятися.
  
  Для виконання роботи потрібно переглянути демонстраційні розв'язання — презентації MS PowerPoint, до яких перейти за гіперпосиланням, прив'язаним до останнього знаку пунктуації в умові завдань. І розглянути подані розв'язання потрібно через призму єдиного способу розв'язання логічних задач:

  • кількість рівнів прийняття гіпотез — це кількість об'єктів (персонажів), щодо властивостей яких роблять припущення;

  • кількість гіпотез на рівні — це кількість припущень щодо відповідного об'єкта (персонажа).

  Якщо припущень немає взагалі, то кількість рівнів прийняття гіпотез дорівнює 0. Відповідь повинна мати один з таких двох виглядів:

  • або «0 рівнів прийняття гіпотез»;
  • або «на рівні 1 ... гіпотез, на рівні 2 — до ... гіпотез» і т.д.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Набуття процедурної компетентності в опануванні алгоритмами у процесі розв’я­зання задач на побудову

Анотація
Огляд теоретичних і практичних аспек­тів навчання розв'язуванню задач на побудову: навіщо потрібно розв'язувати такі задачі і чого не можна уникнути?

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — (бажано при синхронному перегляді відеозапису лекції Олександра Рудика від 21 січня 2018 року на курсах підвищення кваліфікації вчителів математики) ознайомитися з такими матеріалами:

  • перелік базових операцій:

    • побудувати пряму, що проходить через дані дві точки;
    
    
    • побудувати коло за відомими центром і радіусом;
    
    
    • для двох даних прямих:
      • або встановити, що вони збігаються;
      • або встановити, що вони не перетинаються (паралельні);
      • або знайти єдину їхню спільну точку;
    
    
    • для двох даних кіл:
      • або встановити, що вони збігаються;
      • або встановити, що вони не перетинаються;
      • або встановити, що вони дотикаються, і знайти точку їхнього дотику;
      • або знайти дві точки їхнього перетину;
    
    
    • для даних прямої і кола:
      • або встановити, що вони не перетинаються;
      • або встановити, що вони дотикаються, і знайти точку їхнього дотику;
      • або знайти дві точки їхнього перетину;

  • перелік етапів розв'язання:

    • аналіз (умови) — встановлення (усіх можливих) зв'язків між тим, що дано, і тим, що потрібно побудувати. Інколи для побудови математичної моделі достатньо подати рисунок з указанням рівних елементів, перпендикулярних і паралельних прямих;

    • побудова — словесний опис (алгоритм) процесу побудови, проілюстрований одним або кількома рисунками з величинами чи співвідношеннями між ними, заданими в умові завдання. Зазвичай, учень повинен сам обрати довжини відрізків і величини кутів, щоб отримати прийнятну за розмірами ілюстрацію, без порушення типовості — максимальності розмірності простору значень параметрів. Побудова є очевидним наслідком якісно проведеного аналізу;

    • доведення того, що побудована фігура є шуканою. Традиційно цей крок не подають у розв'язанні, якщо таке доведення є безпосереднім наслідком аналізу й алгоритму побудови;

    • доcлідження кількості розв'язків, умов можливості побудови, нетипових випадків значень даних, при яких алгоритм потрібно істотно змінити (з указанням цих змін). Це найскладнійший етап розв'язання.

  • перелік базових задач, у термінах яких описують розв'язання задач на побудову за допомогою циркуля й лінійки;

  • перелік типових задач на побудову за допомогою циркуля й лінійки;

  • традиційні позначення й поняття паралельної та центральної (конічної) проекції:

    • (AB) — пряма, що проходить черед різні точки A і В;

    • [AB) — промінь на прямій (AВ) з початком A, що містить В;

    • [AB] — відрізок з кінцями A і В;

    • (ABC) — площина, що проходить точки A, B, C, що не належать до однієї прямої.

    Означення 1. Нехай у (тривимірному) просторі задано непаралельні площину β і пряму l. Кажуть, що точка B є проекцією точки A при проектуванні на площину β паралельно прямій l, якщо В ∈ β і (AB) || l.
    
    Інакше кажучи, щоб знайти паралельну проекцію точки А, потрібно провести через неї пряму, паралельну l, до перетину з площиною проектування β у точці B.
    
    Означення 2. Нехай у (тривимірному) просторі задано непаралельні площину β і пряму l. Кажуть, що точка B є проекцією точки A при проектуванні на пряму l паралельно площині β, якщо В ∈ l і (AB) || β.
    
    Інакше кажучи, щоб знайти паралельну проекцію точки А, потрібно провести через неї площину, паралельну β і знайти точку перетину її з прямою l.
    
    Попередні два означення описують так зване паралельне проектування. Креслярська справа передбачає використання паралельного проектування на площину з урахуванням певних стандартів, зафіксованих нормативними актами і програмно реалізованими у автоматизованих системах програмування.
    
    Означення 3. Проекція фігури — це множина проекцій точок фігури.
    
    Деякі властивості паралельного проектування:

    • проекція прямої — пряма або точка;

    • проекції паралельних прямих, які не паралельні прямій, вздовж якої проектують, або збігаються, або паралельні;

    • при проектуванні прямої у пряму зберігаються відношення довжин відрізків.

    Означення 4. Нехай у (тривимірному) просторі задано площину β і точку О поза нею. Кажуть, що точка B є центральною (конічною) проекцією точки A на площину β з центром проектування О, якщо В ∈ β і точки A, B, O розташовані на одній прямій.
    
    Інакше кажучи, щоб знайти центральну (конічну) проекцію точки A, потрібно провести через неї та центр проектування O пряму до перетину з площиною проектування β у точці B.
    
    Деякі властивості центрального (конічного) проектування прямих, які можна довести на основі шкільного курсу стереометрії:

    • центральна (конічна) проекція прямої — пряма або точка;

    • центральні (конічні) проекції прямих, які паралельні площині проектування, або збігаються, або паралельні;

    • при центральному (конічному) проектуванні прямої, які паралельна площині проектування, зберігаються відношення довжин відрізків;

    • прямі, що є центральними (конічними) проекціями паралельних прямих однієї площини, які непаралельні площині проектування, перетинаються в одній точці, яку називають точкою сходження;

    • точки сходження прямих, що лежать у одній площині γ, розташовані на прямій перетину площини проектування і площини, що проходить через центр проектування паралельно γ. Якщо площина γ горизонтальна щодо поверхні Землі, то відповідну пряму перетину площин, що містить згадані точки сходження, називають лінією горизонту.

    Перспектива (латинською — бачити наскрізь) — це система зображення простору та предметів на одній площині для створення уявної глибини та об’єму.
    
    Перспектива передбачає використання конічної проекції з урахуванням того, яка частина поверхні зображуваного просторового тіла (предмета) видима, а які — ні. Перелічені вище властивості конічного проектування прямих слугують для допоміжних побудов напрямних ліній, що використовують при побудові зображень;

  • правило: точка перетину прямої і площини є точкою перетину цієї прямої з її проекцією на цю площину;

  • тлумачення обов'язкових складових запису задач на побудову перерізу многогранників, що містить дані точки, на прикладі побудови перерізу піраміди площиною, що містить дані внутрішні точки трьох різних граней;

  • умови завдань на побудову перерізу многогранника, подані рисунком або текстом.

• Завдання для самостійної роботи — контроль результатів навчання — подати словесне формулювання умови й розв'язання однієї задачі зі збірки задач, умови яких подано рисунком.
  
  Номер задачі має відповідати першій літері прізвища слухача в українській абетці таким чином:

   1   2   3   4   5  6    7   8   9  10
  Аа  Бб  Вв  Гг  Ґґ  Дд  Ее  Єє  Жж  Зз
  
  11  12  13  14  15  16  17  18  19  20
  Ии  Іі  Її  Йй  Кк  Лл  Мм  Нн  Оо  Пп
  
  21  22  23  24  25  26  27  28  29  30
  Рр  Сс  Тт  Уу  Фф  Хх  Цц  Чч  Шш  Щщ
  
  33  32
  Юю  Яя

  Технічні вимоги до подання
  
  Подавати архів zip з двох файлів:

  • опис — файлом типу doc, docx, odt, txt чи html — на розсуд виконавця;
  • ілюстрацію — або файлом растрової графіки у форматі png, або файлом векторної графіки типу svg, який можна створити у середовищі редактора векторної графіки Inkskape. В останньому випадку нижній шар ілюстрації утворити даними файлу, завантаженого з умови вказівкою контекстного меню Зберегти зображення як.... Кожний елемент побудови подавати окремим шаром. Шари розташувати у порядку побудови знизу догори. У разі виконання усіх вимог щодо виконання ілюстрації і побажання щодо формату html можна отримати демонстраційне розв'язання задачі, яке вже можна показати учням — див. розв'язання задачі № 31.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Ефективність розв’язання та його оформлення для показникових і логарифмічних нерівностей

Анотація
Модуль висвітлює методи перетворення транцендентних (показникових і логарифмічних) нерівностей в алгебричні відносно основи й аргументів функції. У тому числі, і при наявності модуля. Ці методи зменшують щонайменше удвічі кількість виконуваних дій і запис розв'язання. Це є гарною ілюстрацією того, що навчання математиці може й має йти під гаслом: “Знання математики — це уміння уникати громіздких обчислень і формул”.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання:

  • ознайомитися з авторським прочитанням розділу "Показникові й логарифмічні нерівності" посібника «Початки алгебри, аналізу, аналітичної геометрії і теорії ймовірностей». Тернопіль, Богдан, 2005, 416 с., поданим відеозаписом, що містить такі розділи:

    1. Метод інтервалів (0:45)
    2. Перетворення показникових нерівностей на алгебричні відносно основи й аргумента (6:35)
    3. Перетворення логарифмічних нерівностей на алгебричні відносно основи й аргумента (16:28)
    4. Знак добутку значень логарифмічної функції (21:25)
    5. Приклад розв'язання системи двох логарифмічних нерівностей відносно двох змінних (32:08)
    6. Модуль у логарифмічних нерівностях (36:39)

    Рекомендований темп ознайомлення один розділ протягом дня. Але при потребі його переглянути кілька разів, враховуючи три рівні опанування літературою:

    • таке пишуть;
    • написано правду;
    • зрозуміло, чому автор виклав матеріал саме таким чином.

  • після озайомлення з кожним розділом з інтервалом у тиждень пересвідчитися у засвоєнні матеріалу, розв'язавши приклади, розібрані у відеозаписі, але без підглядування у запис.

• Завдання для самостійної роботи — контроль результатів навчання — подати умову і демонстраційне розв'язання одного завдання на використання методів, поданих у розділах 2-6. Умови мають відрізнятися від поданих у відеозаписі — чим більше відрізняється, тим краще. Текст роботи подати в одному з таких форматів (перелічено у порядку спадання бажаності): html, tex, odt, docx, doc.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Розвиток комбінаторного мислення

Анотація
Вичерпно викладено зміст шкільного курсу комбінаторики із коментарями щодо мети вивчення комбінаторики й методики подання окремих тем відповідно до сучасного стану математики.

Звернення тьютора — у формі pdf-презентації та відео.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з такими матеріалами :

  • Олександр Рудик. Зміст шкільного курсу комбінаторики – за матеріалами посібника: Рудик О.Б. Початки алгебри, аналізу, аналітичної геометрії і теорії ймовірностей. — Тернопіль: Навчальна книга – Богдан, 2005, 416 с.

  • Вишенський В.А., Перестюк М.О., Самоленко А.М. Збірник задач з математики. — Київ, Либідь, 1993, 344 с. — лише §5: умови й відповіді.

  • Дороговцев А.Я., Сільвестров Д.С., Скороход А.В., Ядренко М.Й. Теорія мовірностей. Збірник задач. За загальною редакцією члена-корреспондента АН УРСР Скорохода А.В. — Київ, Вища школа, 1976, 384 с. — лише §2 розділу 1: умови й відповіді — за бажанням.

  Весь навчальний матеріал, глосарій і додатки подано у перелічених матеріалах.

• Завдання для самостійної роботи — контроль результатів навчання — подати:

  • або словесний опис одного (і лише одного!) перебору:
    • чи всіх підмножин 4-елементної множини;
    • чи всіх перестановок 4-елементної множини;
    • чи всіх 2-елементних підмножин 4-елементної множини
    без використання готових схем перебору номерів елементів;

  • або розв'язання однієї (і лише однієї!) із задач: 15; 22; 24 a, b (лише комбінаторно); 39; 71; 72; 79; 84; 89; 90 з переліку

  в одному з таких форматів: html, html + LaTeX, LaTeX або txt.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Відношення подільності

Анотація
Вичерпно викладено зміст шкільного курсу щодо поглибленого вивчення відношення подільності.

Звернення тьютора — у формі pdf-презентації та відео.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з такими матеріалами :

  • Теоретичні основи поглибленого вивчення відношення подільності — див. сторінки 53-78 (IV розділ) посібника Рудик О.Б. Початки алгебри, аналізу, аналітичної геометрії і теорії ймовірностей. — Тернопіль: Навчальна книга – Богдан, 2005, 416 с.

  • Олександр Рудик. Подiльнiсть i коренi многочленiв. Презентацiя у форматi pdf.

  • Вишенський В.А., Перестюк М.О., Самоленко А.М. Збірник задач з математики. — Київ, Вища школа, 1982, 334 с. — лише §1: умови й відповіді.

  • Додаткові задачі: умови й відповіді.

  Весь навчальний матеріал, глосарій і додатки подано у перелічених матеріалах.

• Завдання для самостійної роботи — контроль результатів навчання — подати розв'язання однієї з підзадач а, б, ... додаткових задач № 2, 3 або 4 або довільної із задач № 5-40 в одному з таких форматів: html, html + LaTeX, LaTeX, txt або сканом рукописного тексту .

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Початки мови розмітки тексту з матема­тичними формулами LaTeX

Анотація
LaTeX — найкраща авторська видавнича системи для подання текстів зі складними математичними формулами. Вона стане у нагоді при підготовці завдань до контрольної, підручника чи посібника, наукової роботи (на конкурс МАН). Модуль передбачає огляд найуживаніших службових слів, відображення нестандартних символів, подання рисунків, таблиць, змісту, покажчика. Подано змістовний приклад pdf-презентації з наголосом на структуру подання навчального матеріалу.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з такими матеріалами:

  • Олександр Рудик. Встановлення і перші кроки використання LaTeX // Комп'ютер у школі та сім'ї, 2012, № 1, с. 47-51, № 4, с. 43-47 — опис встановлення при ОС Windows можна відкласти на майбутнє, якщо слухач не збирається найближчим часом встановлювати це ПЗ на свій ПК, а використає online-сервіси для набуття практичних навичок. Щодо власне вказівок LaTeX'у можна обмежитися нумерованими й маркованими списками, індексами і степенями, радикалами й дробами.

  • Олександр Рудик. Векторна графіка в LaTeX заcобами TikZ // Комп'ютер у школі та сім'ї — 2012. — № 7. — С. 43–46, № 8. — С. 35–38.

  • Приклад сторінки коду HTML з використанням мови LaTeX для запису математичних формул без нумерації.

  • Олександр Рудик. Подiльнiсть i коренi многочленiв. Приклад подання навчального матерiалу презентацiєю у форматi pdf, створеної за допомогою пакету beamer з коду LaTeX — лише для охочих.

• Завдання для самостійної роботи — контроль результатів навчання — виконати cамостійну роботу: подати файлі типу tex з текстом контрольної роботи на 5 завдань (тема довільна) зі складними (не в один рядок) математичними формулами.
  
  Такий файл можна створити:

  • або за допомогою встановленого програмного забезпечення — це саме той випадок, коли з ОС Linux істотно менше мороки;

  • або з використанням служб online LaTeX — застосувати останні два слова як ключові для пошукових систем.

  Замість файлу типу tex можна подати файл типу html, змінивши відповідним чином текст розглянутого прикладу сторінки коду HTML.

Примітка. Для коректного копіювання кирилічних літер з документу у форматі pdf потрібно додати вказівку \usepackage{cmap} перед завантаженням пакетів fontenc та babel.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Елементи теорії груп при поглибленому вивченні математики

Анотація
Обґрунтування необхідності долучення елементів теорії груп до курсу (щонайменше, поглибленого) вивчення математики. Демонстрація прийомів ознайомлення з поняттям групи у межах понятійного апарату шкільного курсу математики.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання — ознайомитися з текстом, що містить весь навчальний матеріал, глосарій і додатки. Cамостійно розв'язати усі завдання, подані у тексті. Порівняти свої результати з поданим демонстраційним розв'язанням.

• Завдання для самостійної роботи — контроль результатів навчання — подати розв'язання однієї задачі з переліку завдань для закріплення набутих знань, що не має демонстраційного розв'язання. Формат файлу — довільний з tex, html, odt, docx, що не містить зображення сканованого рукописного тексту.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Система комп'ютерної алгебри Reduce

Анотація
Знайомство з система комп'ютерної алгебри Reduce на рівні практичного використання у межах понятійного апарату шкільного курсу математики. Найімовірніша сфера використання — наукові роботи з математики та фізики здобувачів освіти, пов'язані зі складними (громіздкими) аналітичними обчисленнями. У тому числі й тими, зміст яких виходить за межі шкільного курсу математики. Наприклад, визначення умов стійкості системи за власними числами певної матриці.

Звернення тьютора — у формі pdf-презентації.

Зміст (план) курсу

• Завдання для навчання

  1. Вікрити у середовищі браузера сторінку https://reduce-algebra.sourceforge.io/.

     

     У разі потреби вибрати мову перекладу, усвідомлюючи, що машинний переклад змісту сторінки може виявитися недосконалим чи навіть недоречним (на малюнку нижче REDUCE замінено на ЗМЕНШИТИ).

     

     Клацаючи лівою кнопкою мишки на зображеннях кнопок по лівому й правому краям сторінки, переглянути можливості пітримки система комп'ютерної алгебри Reduce. Обсяг і глибина занурення — на власний розсуд.

  2. Завантажити файл для встановлення системи REDUCE з ресурсу SOURCEFORGE, клацнувши лівою кнопкою мишки на зображенні кнопки з відповідною назвою у лівому нижньому куті сторінки.

  3. Встановити програмне забезпечення:

     • при ОС Ubuntu/Linux Mint:

       • розпакувати завантажений файл (з назвою reduce-complete_6860_amd64.tgz станом на 1 лютого 2025 року);

       • отримані після розпанування теки etc і usr скопіювати у кореневу теку системи /, суміщаючи з наявними;

       • пересвідчитися у можливості перегляду опису з допомогою браузера Firefox,

         

         виконавши вказівку терміналу:
         
         firefox /usr/share/reduce/cslbuild/csl/reduce.doc/index.html

       • пересвідчитися у можливості відкриття вікна програми, виконавши вказівку терміналу:
         
         /usr/lib/reduce/cslbuild/csl/reduce

       • пересвідчитися у дієздатності програми:
         • набрати на клавіатурі вираз (a+b)**3;
         • натиснути клавішу Enter;
         • отримати вікно такого вигляду:
         
         
     

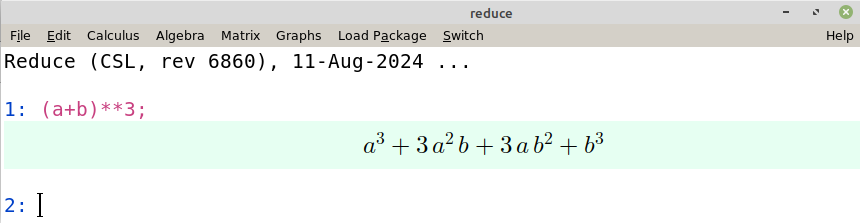
     • при ОС Windows: запустити на виконання завантажений файл (з назвою Reduce-Setup_6860.exe станом на 1 лютого 2025 року) і вказати теку встановлення. Наприклад, D:/Reduce_installed;

     • пересвідчитися у можливості перегляду опису з допомогою браузера, відкривши у його середовищі файл D:/Reduce_installed/lib/csl/reduce.doc/index.html;

     • пересвідчитися у можливості відкриття вікна програми, використавши вказівку Пуск / Reduce / CSL Reduce;

       
     
     
     • пересвідчитися у дієздатності програми:
       • набрати на клавіатурі вираз (a+b)**3;
       • натиснути клавішу Enter;
       • отримати у вікні програми вираз для кубу суми двох доданків.

  4. Прочитати текст розділу 5. Виконання завдань / 6. Вивчення нового матеріалу розробки уроку з інформатики для 8 класу. Використовуючи посилання у згаданому вище файлі index.html, прочитати опис понять з переліку. Спробувати самостійно розв'язати задачі 1-14, подані у тексті розробки, використовуючи Reduce. Порівняти свої результати з поданим у демонстраційним розв'язанням.

• Завдання для самостійної роботи — контроль результатів навчання — подати одним текстовим файлом розв'язання з допомогою Reduce з природним форматом виведення (on nat) таких завдань.

  1. Записати многочлен 5 степеня з цілими коефіцієнтами, що має такі корені: 2, −1/3, 4/5, −7/6, 8/9.

  2. Розв'язати рівняння 2520x⁵ + 612x⁴ − 6022x³ + 567x² + 3868x − 1440 = 0.

  3. Обчислити y" при y = x⁴ cos(x³).

  4. Знайти первісну функції y = ln x.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Аналіз статистичних даних і критерії прийняття гіпотез

Анотація
Знайомство з базовими поняттями аналізу даних і непараметричних критеріїв прийняття гіпотез, поширеними у гуманітарних дослідженнях.

Звернення тьютора — у формі pdf-презентації — щодо потреби удосконалювати методику навчання математиці і вивчення ефективності такого удосконалення.

Зміст (план) курсу

• Завдання для навчання:
  • прочитати конспект лекцій, що містить весь навчальний матеріал і глосарій;
  • пересвідчитися у доступності таблиць, необхідних для опрацювання даних.

• Завдання для самостійної роботи — контроль результатів навчання — описати приклад дослідження, пов'язаного з освітою: що вивчати, з якою метою, які дані та у якій формі збирати. Формат файлу — довільний з tex, html, odt, docx, що не містить зображення сканованого рукописного тексту.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.

Початки теорії автономних систем

Анотація
Знайомство з базовими поняттями теорії динамічних систем, необхідними для осмисленого математичного моделювання з допомогою систем звичайних диференціальних рівнянь. Для керівників гуртків і керівників конкурсних робіт МАН, пов'язаних з математичним моделюванням з допомогою систем звичайних диференціальних рівнянь.

Звернення тьютора — у формі pdf-презентації — щодо потреби удосконалювати методику навчання математиці і вивчення ефективності такого удосконалення.

Зміст (план) курсу

• Завдання для навчання для набуття знань, достатніх для надання консультацій здобувачам освіти при ознайомленні з цими самими матеріалами:

  • прочитати розділи 9.7-10, 12.1-5, 13.1-5, 14.1-2 посібника, щоб згадати частину університетського курсу математики у тому обсязі, який можна подати при поглибленому/профільному вивченні матики у закладі загальної середньої освіти. Цей крок не є необхідним при наявності добротних знань і навичок з перелічених розділів;

  • прочитати конспекти лекцій, що містять весь навчальний матеріал і глосарій:
    • Початки теорії автономних систем;
    • Система Лоренца як приклад динамічної системи зі складною поведінкою.
  
  
  

• Завдання для самостійної роботи — контроль результатів навчання:

  • або лише для одного із завдань 1-3 створити програму однією з мов: С++, C#, Java, Javascript, Pascal, PHP, Python, Ruby для системи звичайних диференціальних рівнянь, що має атрактор з дробовою розмірністю. Наприклад, для системи Лоренца з такими значеннями параметрів: σ = 10, b = 8/3, r = 28

  • або виконати лише одне із завдань 4-5 для нелінійної системи звичайних лінійних рівнянь, відмінної від системи Лоренца і без розділення змінних.

  Формат файлу — довільний з tex, html, odt, docx, що не містить зображення сканованого рукописного тексту.

  1. З даної точки рухатися заданий проміжок часу, після чого для заданої лінійної комбінації l координат з даними коефіцієнтами побудувати графік (l_j, l_j+1), де l_j, l_j+1 — послідовні значення локальних максимумів лінійної комбінації l вздовж траєкторії потоку. Для збільшення точності знаходження можна, але не обов'язково, використати кубічний слайн — наближення кривою, що сполучає 2 точки по різні боки поверхні dl/dt = 0, а похідна за часом t у цих точках збігається з вектором поля напрямків досліджуваної системи. Або хоча б лінійним сплайном.

  2. З даної точки рухатися заданий проміжок часу, після чого для обчислити характеристичні показники Ляпунова до того моменту, поки перші три відмінні від нуля цифри найбільшого показника перестануть змінюватися.

  3. Подати на 3 файлах растрової графіки розміру 1000×1000 пікселів:
     • прямокутну проєкцію на деяку площину початкової множини на 2-вимірної поверхні;
     • проєкцію на ту саму площину результату однократного відображення Пуанкаре початкової множини для потоку у 3-вимірному просторі. Образ відображення Пуанкаре разом з деяким своїм околом початковій множині;
     • проєкція на ту саму площину результату двократного відображення Пуанкаре початкової множини для того самого потоку.
     Використати градієнтне заповнення для розпізнавання образів різних частин початкової множини: точку поверхні та її образи подавати одним кольором. Для контура використати колір, відсутній у градієнтному заповненні.
  
  
  4. Провести аналіз на наявність і стійкість особливих точок залежно від значень параметрів поля напрямків у просторі, розмірність якого перевищує 2. Будуть зараховані:
     • або тексти з повними аналітичними викладками;
     • або тексти з результатами й кодом мовою аналітичних обчислень, з допомогою яких отримано ці результати.

  5. Довести існування обмеженої замкненої множини, інваріантної відносно дії потоку у просторі, розмірність якого перевищує 2.

Прохання пройти анкетування за адресою https://forms.gle/Taw4J7xRyRGPfcPY8 щодо участі педагогічних працівників у курсах кафедри природничо-математичної освіти і технологій.